Andrew J. Moodie

Andrew J. Moodie

Assistant Professor, Texas A&M Geography. Quantitative surface processes and geomorphology to enable sustainable landscapes.

Research

Predicting deltaic avulsion timing and location

Figure 1: Yellow River delta shortly after an avulsion relocated the main channel from the north to the east. Image: Landsat, 1978.

Project overview

Deltaic avulsion causes flooding and channel relocation. Predicting when and where avulsions occur will improve landscape stability for society living on a delta. This project uses the Yellow River delta as a case study, so to identify sustainable river-engineering practices, and apply these lessons to the management of deltaic landscapes globally.

This research has been supported by an NSF Graduate Research Fellowship from 2016–2019 and an international NSF Coastal SEES grant.

Introduction

River avulsion, the process of sudden channel relocation (Slingerland & Smith, 2004; Hajek & Wolinsky, 2012), presents a dichotomy to delta sustainability: the unanticipated civil disruption associated with flooding and channel relocation is at odds with society’s desire for landscape stability, yet channel engineering that restricts mobility and floodplain connectivity diminishes sediment dispersal necessary to sustain deltas and coastlines (Giosan et al., 2014; Tessler et al., 2015).

Delta lobe building gif from the Yellow River delta.
Figure 2: Yellow River delta progradation through a summer of river flooding. In this 4 month period, the delta front moved forward more than 4 km and approximately 20 km2 of new subaerial land was developed.

The Yellow River, China (Figure 2), is an end-member fluvial system as it is characterized by very high suspended sediment concentrations, that lead to frequent deltaic avulsions (van Gelder et al., 1994; Wang & Liang, 2000). For example, the primary channel of the Yellow River delta avulses approximately every 7–10 years, whereas many lowland fluvial-deltaic systems require tens to thousands of years between avulsions (Jerolmack & Mohrig, 2007). Figure 2 demonstrates shows that the high sediment load of the Yellow River leads to rapid deltaic lobe progradation.

Methods

This study presents a novel numerical model that explicitly accounts for multiple deltaic lobe-building cycles and delta planform growth. The numerical model is fundamentally rooted in physical relationships and can be summarized by three pseudo-equations. First, the conservation of water mass in the channel dictates the flow velocity (\(U\)):

\[U = Q / A,\]

from the water discharge (\(Q\)) and channel cross-sectional area (\(A\)). Next, the sediment transport (\(q_s\)) is computed:

\[q_s \approx \tau^n\]

for a shear-stress (\(\tau\)) that depends on the flow velocity and an exponent (\(n\), a parameter). The spatial sediment flux gradient (\({\partial q_s}/{\partial x}\)) drives a temporal change in channel bed elevation (\(\eta\)):

\[\frac{\partial \eta}{\partial t} \approx -\frac{\partial q_s}{\partial x}\]

which then provides a feedback, altering the channel cross-sectional area. This set of inter-related equations is the foundation of morphodynamic modeling.

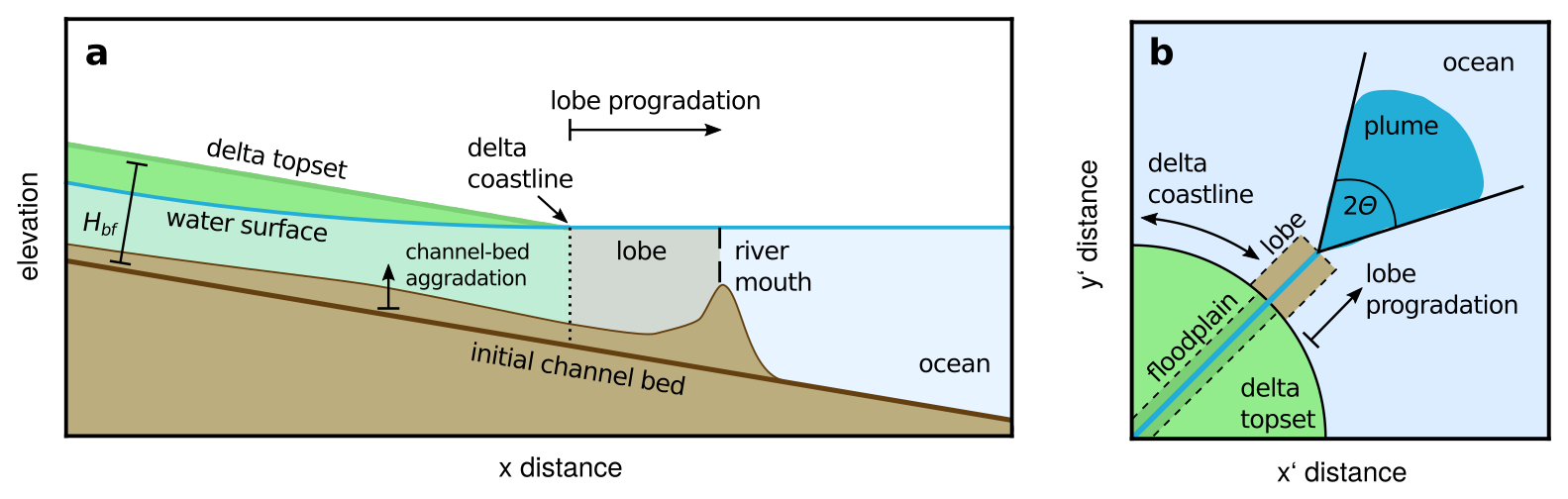
Figure 3: Model schematic, depicting a) the channel long profile and b) the delta planform. Each component of the numerical model is fundamentally rooted in physical relationships.

In the numerical model developed through this research, a systematic downstream decrease in sediment flux causes a deltaic lobe to form near the channel outlet (Figure 3). The model approximates deltaic lobe progradation via a channel-constriction mechanism, that provides realistic constraint on the timing and rate of lobe development.

Insights

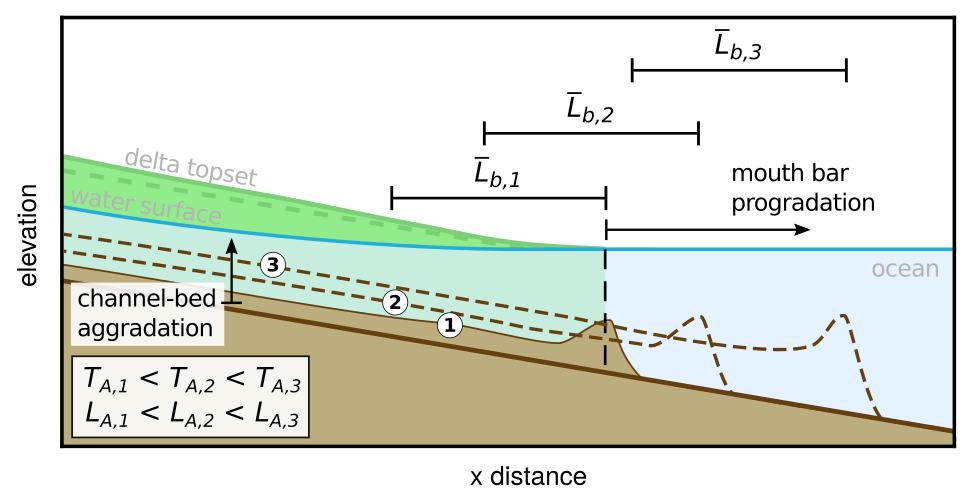
Figure 4: From time 1 to 3, lobe progradation drives upstream aggradation. In turn, upstream aggradation induces avulsions farther upstream than without lobe progradation.

The development of deltaic lobes is found to drive upstream channel bed aggradation in response to reducing fluvial slope. In turn, upstream bed aggradation causes avulsions less frequently and farther upstream than is realized in conditions that do not produce lobes. Increasing low-to-flood-flow disparity increases erosion at the mouth and drives lobe progradation, which in turn shifts the avulsion location upstream. Thus, the location of an avulsion is sensitive to the superelevation threshold, because larger lobes develop when the superelevation threshold is increased.

Publications generated by this research

  1. Moodie, A. J., Nittrouer, J. A., Ma, H., Carlson, B. N., Chadwick, A. J., Lamb, M. P., & Parker, G. (2019). Modeling Deltaic Lobe-Building Cycles and Channel Avulsions for the Yellow River Delta, China. Journal of Geophysical Research: Earth Surface, 124(11), 2438–2462. doi: 10.1029/2019JF005220
  2. Chadwick, A. J., Lamb, M. P., Moodie, A. J., Parker, G., & Nittrouer, J. A. (2019). Origin of a Preferential Avulsion Node on Lowland River Deltas. Geophysical Research Letters, 46(8), 4267–4277. doi: 10.1029/2019GL082491

References

  1. Slingerland, R., & Smith, N. D. (2004). RIVER AVULSIONS AND THEIR DEPOSITS. Annual Review of Earth and Planetary Sciences, 32(1), 257–285. doi: 10.1146/annurev.earth.32.101802.120201

  2. Hajek, E. A., & Wolinsky, M. A. (2012). Simplified process modeling of river avulsion and alluvial architecture: Connecting models and field data. Sedimentary Geology, 257-260, 1–30. doi: 10.1016/j.sedgeo.2011.09.005

  3. Giosan, L., Syvitski, J., Constantinescu, S., & Day, J. (2014). Climate change: Protect the world’s deltas. Nature, 516(7529), 31–33. doi: 10.1038/516031a [link]

  4. Tessler, Z. D., Vörösmarty, C. J., Grossberg, M., Gladkova, I., Aizenman, H., Syvitski, J. P. M., & Foufoula-Georgiou, E. (2015). Profiling risk and sustainability in coastal deltas of the world. Science, 349(6248), 638–643. doi: 10.1126/science.aab3574

  5. van Gelder, A., Berg, J. H. van den, Cheng, G., & Xue, C. (1994). Overbank and channelfill deposits of the modern Yellow River delta. Sedimentary Geology, 90(3–4), 293–305. doi: 10.1016/0037-0738(94)90044-2

  6. Wang, Z.-Y., & Liang, Z.-Y. (2000). Dynamic characteristics of the Yellow River mouth. Earth Surface Processes and Landforms, 25(7), 765–782. doi: 10.1002/1096-9837(200007)25:7<765::AID-ESP98>3.0.CO;2-K

  7. Jerolmack, D. J., & Mohrig, D. (2007). Conditions for branching in depositional rivers. Geology, 35(5), 463. doi: 10.1130/G23308A.1

Updated: