Pint glass short-pours
Have you ever gotten a short pour in your pint glass at the bar but not said anything? Well, after reading this, you may decide you want to say something next time. I’m not the first one to look at the point I’m making here, but I didn’t like the way others have presented it, and wanted to run the numbers myself anyway. The problem is to determine how much beer you are really missing out on, by missing that top bit of the pour.
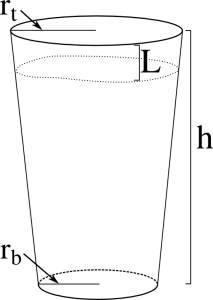
For a theoretical pint glass, the volume of the glass increases with increasing h non-linearly from the base of the glass to the top. This is because the area of a circle is defined by \(\pi r^2\), where r changes linearly along the glass height (\(h\)) from \(r_b\) to \(r_t\). \(L\) represents the vertical length of glass not filled with beer, measured down from the top of the glass.
I approached this problem two ways. First, I set up some simple relations in Matlab, and then numerically estimated the integral to a high spatial resolution, to determine how the volume of liquid in the glass changes with increasing h. I defined the glass geometry by crudely measuring a pint glass, and then fudging the measurements such that volume obtained for the full glass was 16 oz (one pint). Second, I actually filled my glass with 1 oz. slugs of water, and measured the height of the liquid in the glass. Figure 1 shows the modeled and experimental results.
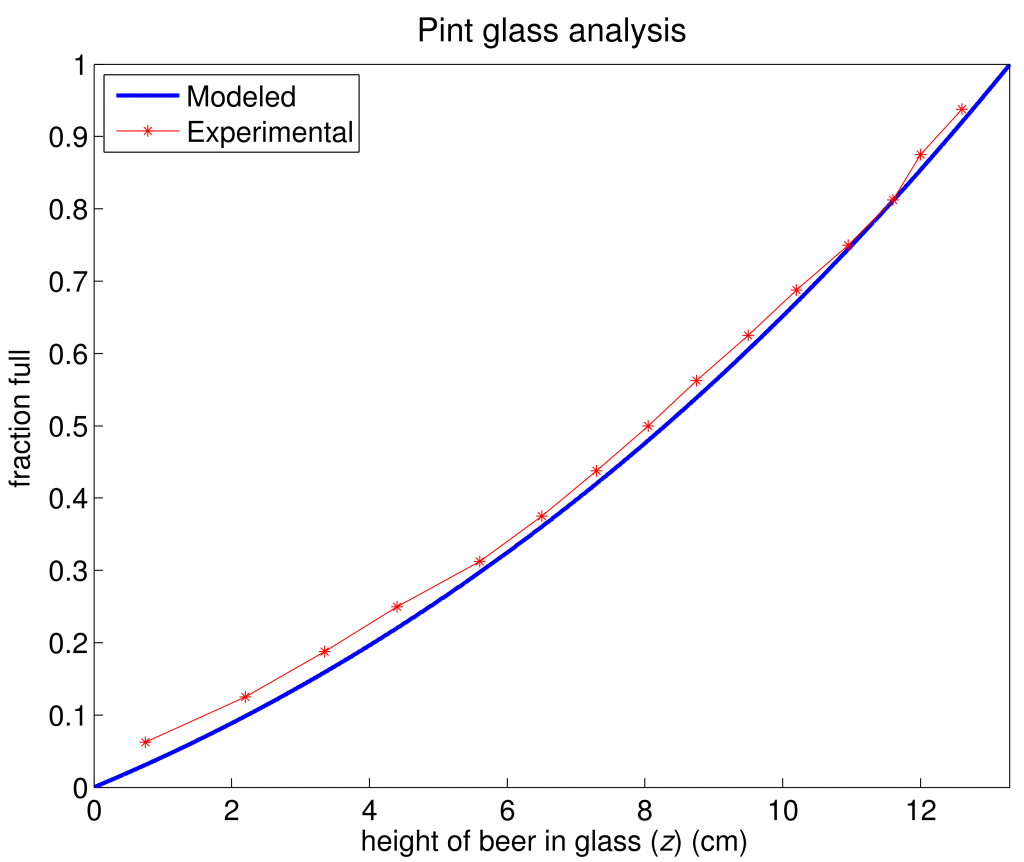
Since the experimental results closely overlay the model results, it is valid to assume the model calculations are accurate and reflect an actual pint glass, so I will proceed only considering the modeled results.
It’s immediately clear (and consistent with our expectation) that the top of the glass is where most of the liquid is held. This is seen in the data with the line slope; a shallow slope in the bottom of the glass means that an increase in the height of liquid equals a small percentage of total volume, whereas at the top of the glass, the same increase in height accounts for a much larger percentage of total volume. This has everything to do with the fact that the cross sectional area of the glass increases with increasing height:
\[A_h = \pi {r_h} ^2\]However, to address the question at hand—how much does a short pour really cheat you—lets look at Figure 2.
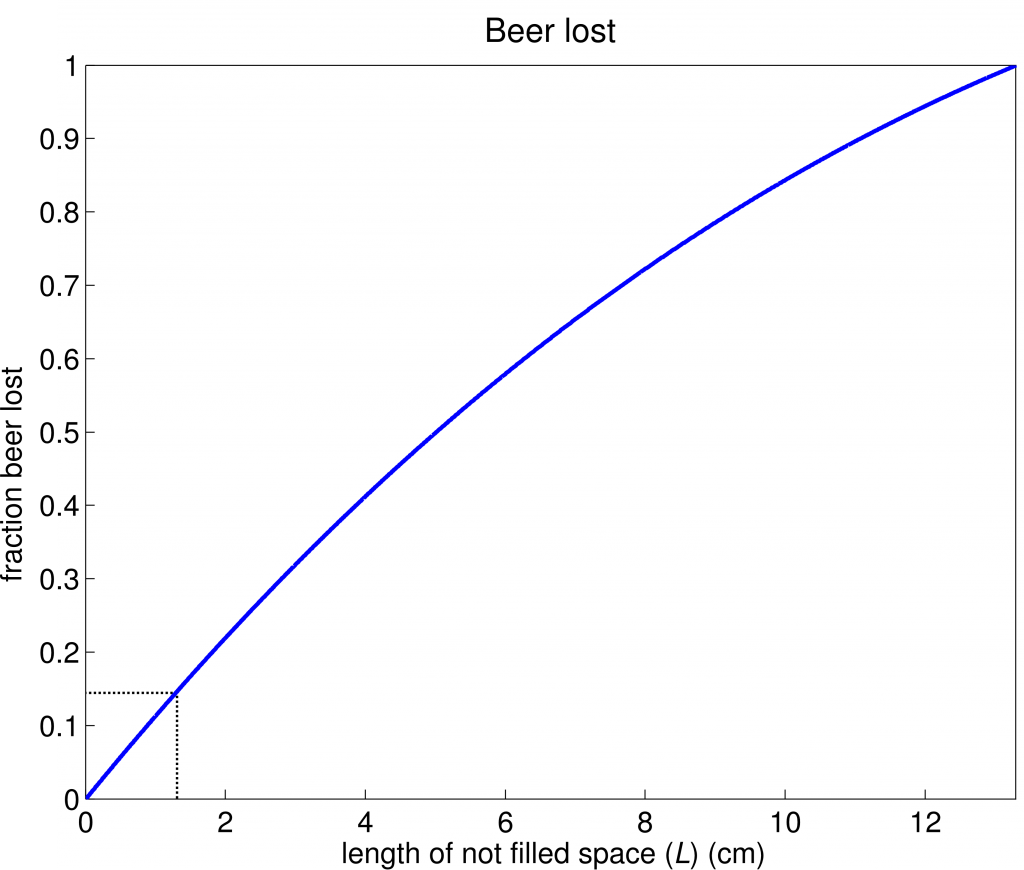
You can see that for a pour in which the top 1/2 inch (1.27 cm) is left empty, the drinker missed out on about 15% of the total volume of the pint-sized beer he paid for! If you are a regular at a hypothetical bar that short pours, every 7 beers you buy, you would be paying for a beer you never got to drink. Now, maybe your bartender isn’t leaving 1/2 inch of empty space at the top of your glass (although I have had it happen), but I do hope that you may think twice about not saying anything if you’re given a bad pour in the future.
Following a suggestion from /u/myu42996: fraction per fraction