The Rouse-Vannoni-Ippen concentration profile interactive module

I have made another interactive GUI toy model thing for the teaching of the Rouse concentration profile. The activity is really simple right now, but I may add more features in the future. You can see the source code and download the module here.

You can specify the grain size and shear velocity (two of the major controls on the Rouse profile) and see how the profile responds in a simplified model (helpful for teaching) and the full Rouse model.

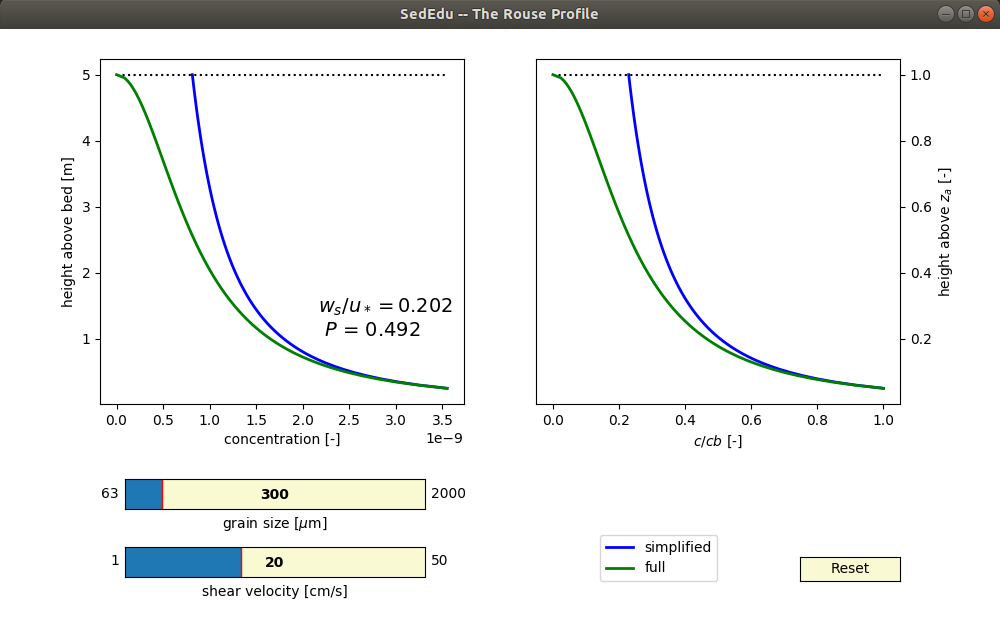
The simplified model is useful for teaching the mechanics of the concentration profile and can be defined as:

\[\frac{c}{c_b} = \left[ \frac{b}{z} \right]^{Z_R}\]

where \(c\) is the concentration at height above the bed \(z\), \(c_b\) is a known reference concentration defined at height \(b\) above the bed, and \(Z_R\) is the Rouse number given as:

\[Z_R = \frac{w_s}{\alpha\kappa u_*}\]

where \(w_s\) is the settling velocity of the grain size in question, \(\alpha\) and \(\kappa\) are constants equal to 1 and 0.41, and \(u_*\) is the shear velocity.

You can see from the form of this simplified model how, for a constant Rouse number, the profile is an exponential decay from the reference concentration. It is also easy to see how changing the Rouse number, through a change in grain size (settling velocity) or shear velocity will change the rate of decay.

The full model has just an additional term to consider, but has the same basic exponential decay form. Here, H is just the total flow depth.

\[\frac{c}{c_b} = \left[ \frac{(H-z)/z}{(H-b)/b} \right]^{Z_R} \\ Z_R = \frac{w_s}{\alpha\kappa u_*}\]

The module uses the Garcia-Parker entrainment relation to calculate near-bed concentration, and used the Ferguson-Church relation for settling velocity.

Link to the respository code: https://github.com/sededu/rouse_model_toy