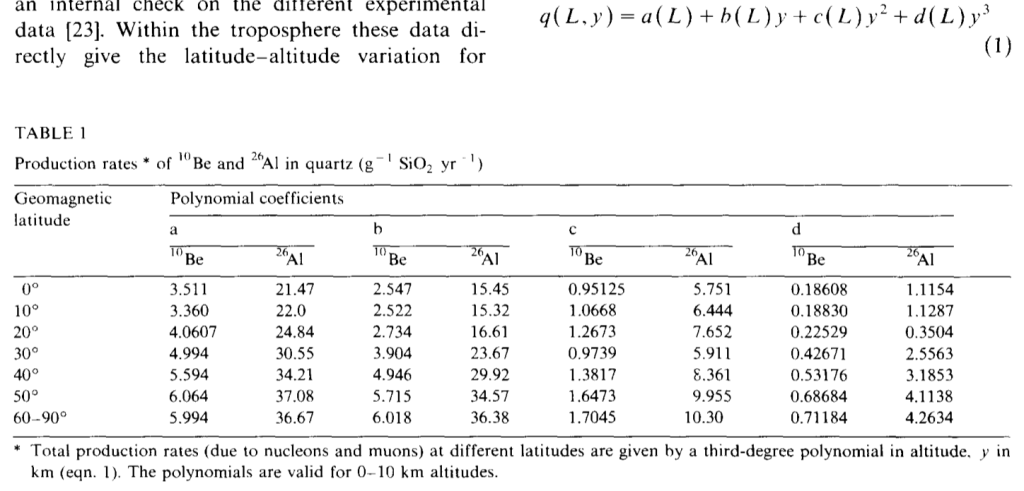
Lal, 1991 in situ 10-Be production rates

¹⁰Be is a cosmogenic radioactive nuclide that is produced when high energy cosmic rays collide with nuclides and cause spallation. ¹⁰Be is produced in the atmosphere (and then transported down to the surface) as “meteoric”, and produced within mineral lattices in soil and rocks as “in situ”. In 1991, Devendra Lal wrote a highly cited paper about the physics of in situ produced Beryllium-10 (¹⁰Be). In the paper he lays out an equation for the production of in situ ¹⁰Be (q) based on latitude and altitude. I’m currently working on an idea I have for using cosmogenic nuclides as tracers for basin scale changes in uplift rate, so I wanted to see what his equation looked like applied. The equation is a third degree polynomial, with coefficients that depend on latitude (L), and direct dependency on altitude (y).

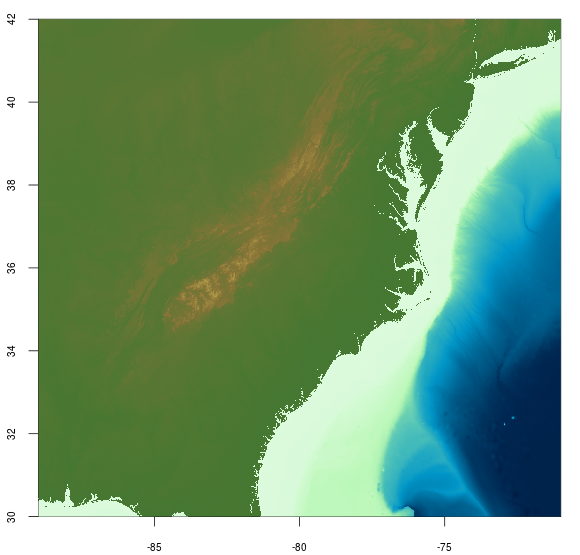
I grabbed an old raster (GEBCO 2014 30 arc second) I had laying around for Eastern North America and plotted it up. First, the elevation map (obviously latitude is on the y-axis…)

Elevation map for ENAM.

And then apply the Lal, 1991 equation and find

Plotting Lal's 1991 in situ production rate equation for ENAM. Green-to-red increasing production rate. Production rate = NA in water.

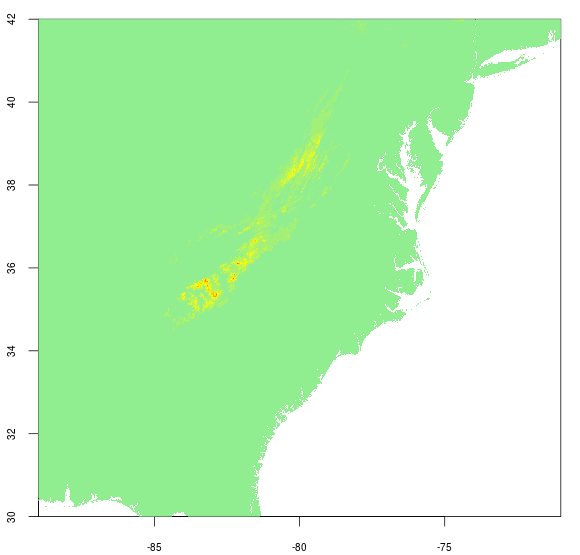
I think the interesting observation is for how little of the mapped area there is any significant change in the production rate. Maybe this should be obvious since the polynomial has direct dependence on altitude and altitude doesn’t change that much in most of the map. Further the dependence of latitude is not all all observable with this map; perhaps because the latitude range is not very large, or the coefficients never change by more than an order of magnitude anyway. Next time, maybe a world elevation map! Not sure my computer has enough memory…

You can grab the code I used from here and Lal’s paper from here.