Density stratification in fine-grained rivers

2017 was the year of my first talk at the fall meeting of the American Geophysical Union. It was pretty exciting and I was extremely nervous. In the end, it went okay, and I was able to present my work to a broad range of scientists. I presented my ongoing research based on field survey of the Yellow River, China during flood.

I hypothesized that the river would exhibit a density stratification in the flow. Density stratification occurs in a river because the entrainment of sediment into the flow affects the properties of the flow in bulk. I’ll explain with the help of a few graphics below. The below image is a profile of an open channel flow (thick black line is the channel bed) and the top of the graphic is the water surface.

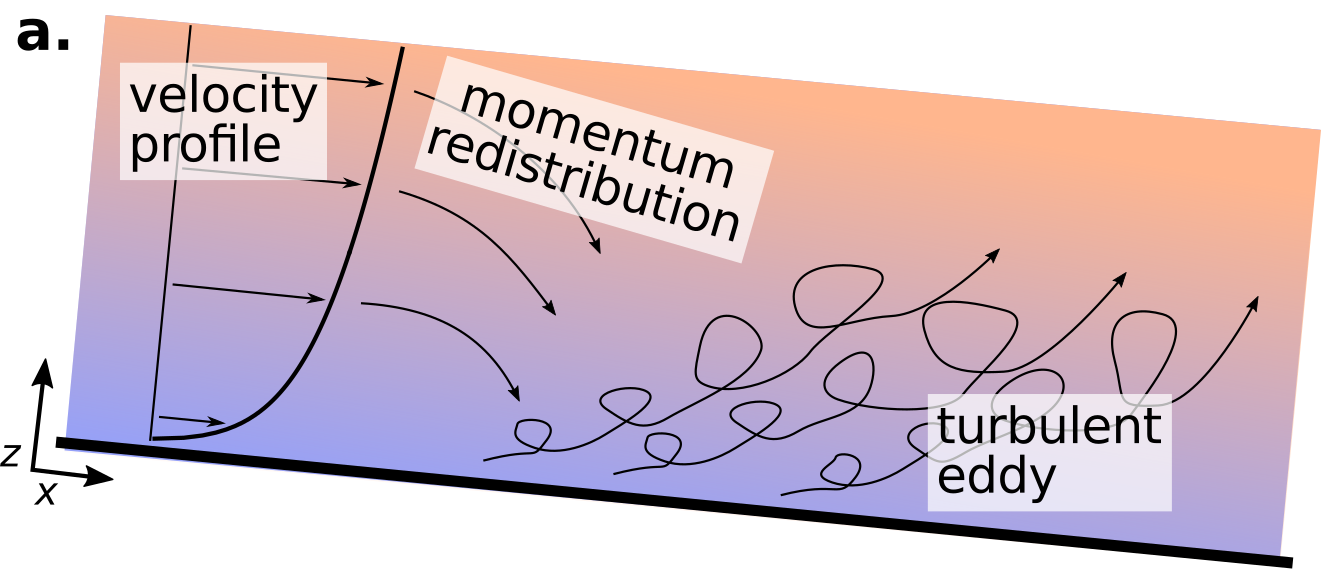
The velocity profile of a steady and uniform open channel flow is well described by the logarithmic “law-of-the-wall” or log-law. This log-law takes the form of:

\[\frac{u}{u_*} = \frac{1}{\kappa} \ln \left( \frac{z}{z_0} \right)\]

which predicts time-averaged velocity (\(u\)) as a function of the shear velocity (\(u_*\)) and the log of the height above the bed (\(z\)). \(z_0\) is a reference height very near the bed, and \(\kappa\) is a constant. The equation, evaluated over the flow depth is shown on the left side of figure a. The implication of higher velocities near the surface means that momentum (\(\rho=mv\)) of the flow is higher near the flow surface than the bed. This condition is unstable, so momentum is redistributed from the surface to the bed through mass transfer. When the flowing mass of high momentum fluid reaches the bed, it dissipates, forming turbulent eddies that shed off the channel bed and move up into the water column.

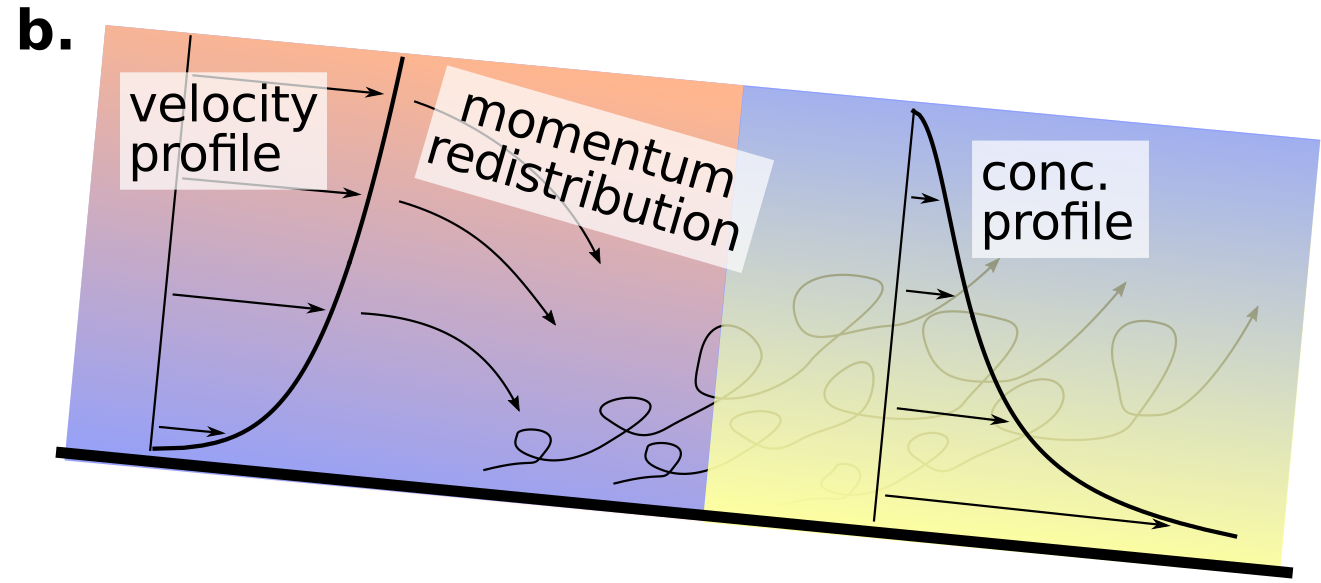
The turbulent eddies coming off the channel bed cause sediment to be entrained into the flow and brought up from the bed towards the surface. The vertical distribution of sediment through the water column depends on the size of particles and the entraining velocity and can be estimated by the exponential Rouse equation.

\[\frac{c}{c_b} = \left[ \frac{(H-z)/z}{(H-b)/b} \right]^{Z_R} \\ Z_R = \frac{w_s}{\alpha\kappa u_*}\]

which predicts time-averaged concentration (\(c\)) as a function of the time-averaged near-bed concentration (\(c_b\)) as a function of the height (\(z\)) above the bed (\(b\)) to the flow depth (\(H\)) and the Rouse number (\(z_R\)) which balances the settling velocity of particles (\(w_s\)), to the entraining shear velocity (\(u_*\)). The Rouse equation and log-law work well only in dilute suspensions, that is, flows in which the concentration of sediment is small enough to have no feedback on the flow.

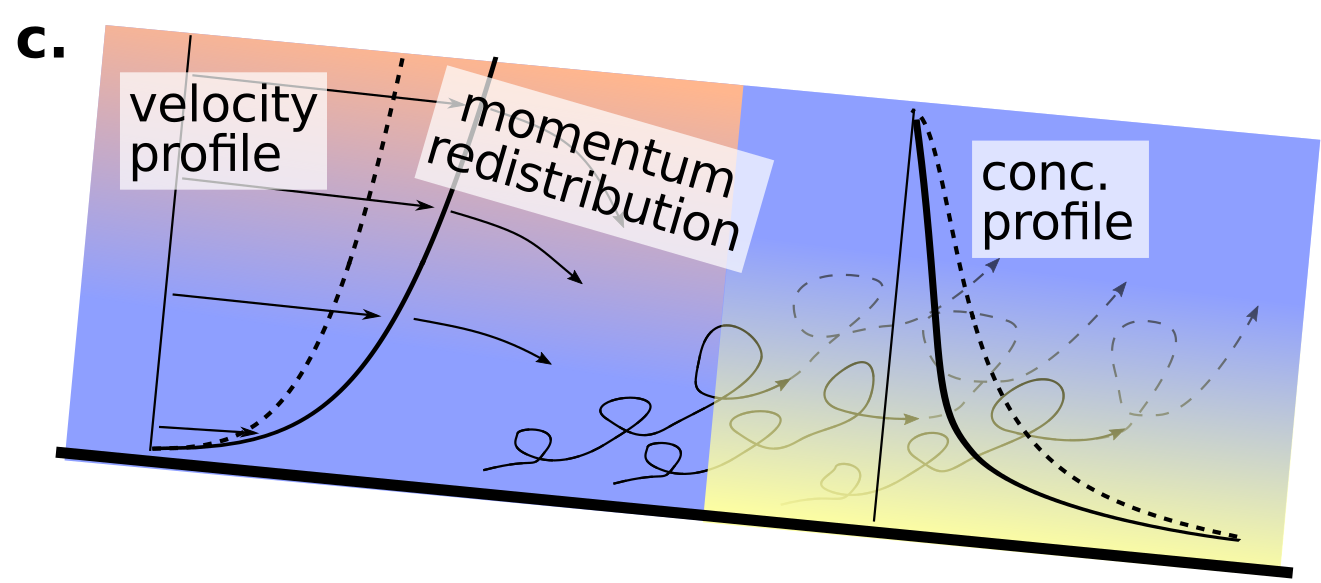
In flows where the sediment concentrations are significant enough near the bed to have a feed back on the system a density stratification develops. In short, the high concentration of sediment prevents momentum redistribution from the surface fully reaching the bed, which has the net effect of reducing sediment suspension and enhancing flow velocities near the surface.

Because sediment transport (\(q_s\) is width-averaged transport) is the product of the velocity and concentration profiles integrated over the flow depth:

\[q_s = \int^H u(z)c(z) dz\]

Density stratification significantly alters total sediment transport rates in fine-grain rivers. My ongoing research in this field is trying to resolve precisely what conditions lead to the development of a density stratification in the river.

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No.1450681. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation.